
Fast-moving scenes have always challenged 4D reconstruction systems. Most camera arrays operate at just 15–30 frames per second (FPS), making it nearly impossible to capture rapid, complex movements accurately. While high-speed cameras exist, they’re expensive and require enormous bandwidth for data transmission.
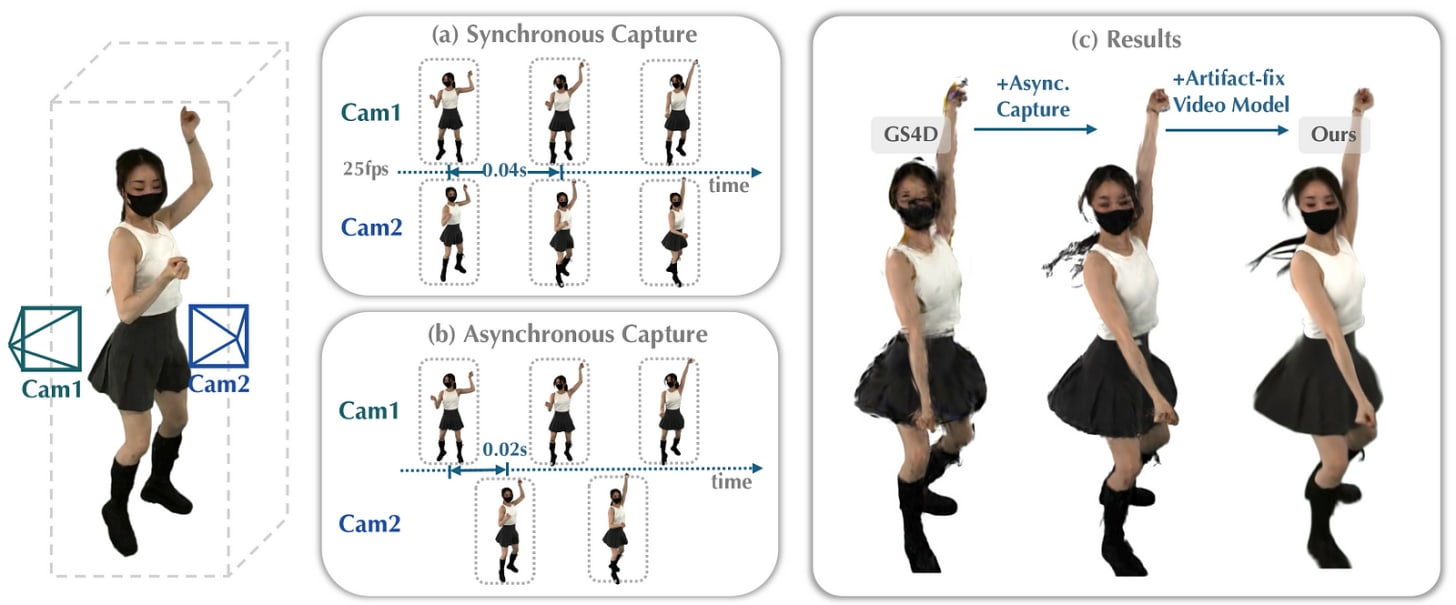
Now, researchers have developed a clever solution that achieves high-quality reconstruction of fast-dynamic scenes without specialized hardware. Their approach, called 4DSloMo, combines two key innovations: an asynchronous capture method that dramatically increases effective frame rate, and a video diffusion model that fixes artifacts created by this novel capture technique.
The Current State of 4D Reconstruction Technology
Dynamic 3D Reconstruction
Most current 4D systems require synchronized multi-view videos as input. These methods typically use radiance field models (like Neural Radiance Fields or 3D Gaussian Splatting) as the foundation, then apply various deformation techniques to capture motion. However, these approaches struggle with temporal interpolation between frames.
The hardware limitations are significant — DNA-Rendering captures at just 15 FPS, while ENeRF-Outdoor and Neural3DV achieve only 30 FPS. These rates fall far short of what’s needed to capture fast-moving subjects like dancers, athletes, or even flowing fabric.
Several approaches have attempted to enhance 4D modeling’s temporal capabilities. For example, TimeFormer uses a transformer module to improve deformable 3D Gaussians, but this enhancement doesn’t provide enough information to reconstruct complex, rapid motions accurately.
Sparse View Scene Reconstruction
Asynchronous capture creates another challenge: at any given timestamp, fewer camera viewpoints are available. This relates directly to sparse view reconstruction, a notoriously difficult problem due to limited input views creating incomplete or ambiguous scene representations.
Recent solutions have incorporated regularization techniques and additional supervision signals. For instance, Freenerf uses depth regularization to improve reconstruction quality from sparse views, while SPARF leverages optical flow from pre-trained models for additional constraints. Similarly, Monosdf integrates depth and normal maps as supplementary supervision signals to enhance geometric accuracy.
3D/4D Reconstruction with Diffusion Models
Recent advances in diffusion models have revolutionized 3D and 4D applications. The pioneering work ReconFusion trained a novel view synthesis diffusion model that conditions on sparse input views, then uses a Score Distillation Sampling (SDS) style optimization for novel view supervision.
Follow-up approaches like Efficient4D: Fast Dynamic 3D Object Generation have integrated diffusion models with NeRF or 3D Gaussian Splatting. More efficient methods like Deceptive-NeRF first render pseudo-images from sparse-view 3D representations, then use diffusion models to enhance these views without querying the diffusion model at every optimization step.
The 4DSloMo Approach: Breaking the Frame Rate Barrier

4D Gaussian Splatting
The foundation of 4DSloMo is 4D Gaussian Splatting (GS4D), which represents dynamic 3D scenes by introducing a time dimension to anisotropic 3D Gaussians. Each 4D Gaussian is defined by its mean vector and covariance matrix, with spatial coordinates (x,y,z) and a temporal coordinate (t).


